Overview

The Omnidirectional Balancing Unicycle Robot (OmBURo) is a robotic system developed at the Robotics and Mechanisms Laboratory (RoMeLa). OmBURo is a robot that was designed as a mobility mechanism in tight spaces shared with people. In order to operate in the close-spaced environment, OmBURo operates in the close-spaced environment with humans by moving omnidirectionally and dynamically balancing based on the principle of dual-axis wheeled inverted pendulum. OmBURo uses a pair of servo motors to drive one large wheel and a set of rollers along the circumference of the large wheel, allowing for omnidirectional movement. Additionally, by using a single wheel for mobility, OmBURo is capable maneuvering dextrously with a small footprint, which is invaluable in tight-spaces. Without using additional motors or other hardware components to the system, I extended the work on OmBURo by analyzing the dynamic factors that influence the orientation, specifically the yaw, of OmBURo and designed a cascaded multi-loop controller to track a desired yaw rate, using a dynamic phenomenon called gyroscopic precession.

Gyroscopic Precession

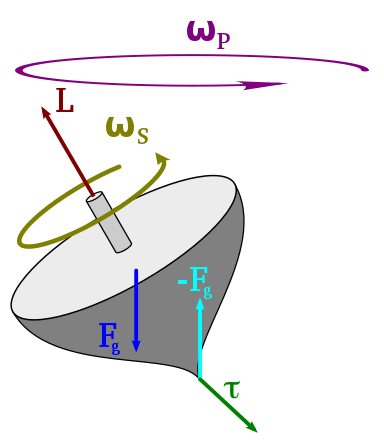
Gyroscopic precession is the relationship between the angular momentum of an object and the torque applied to it.

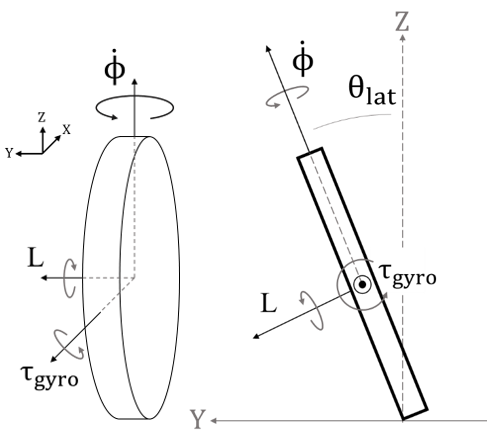
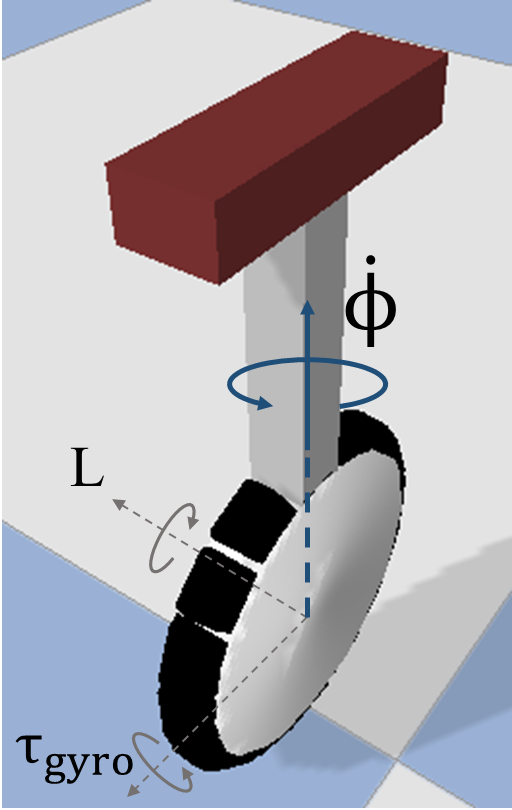
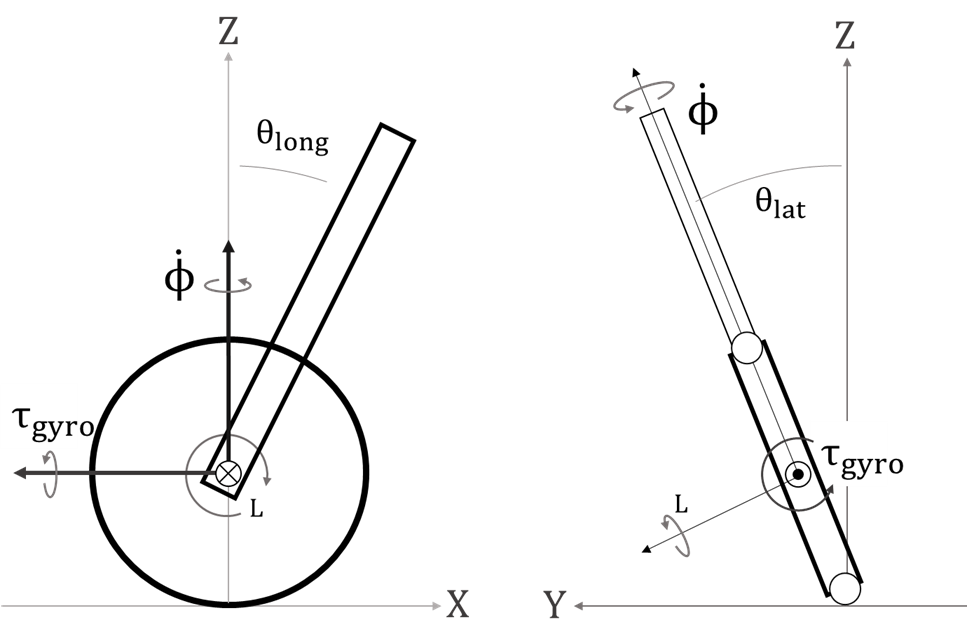
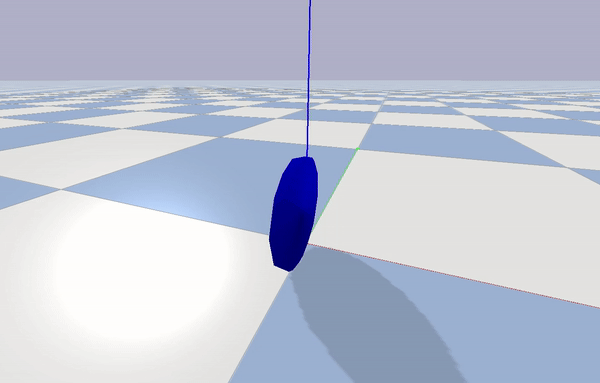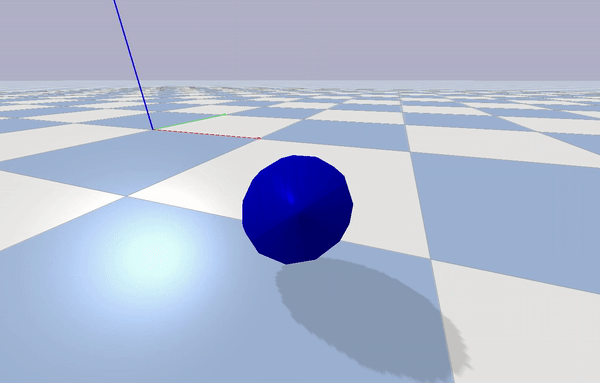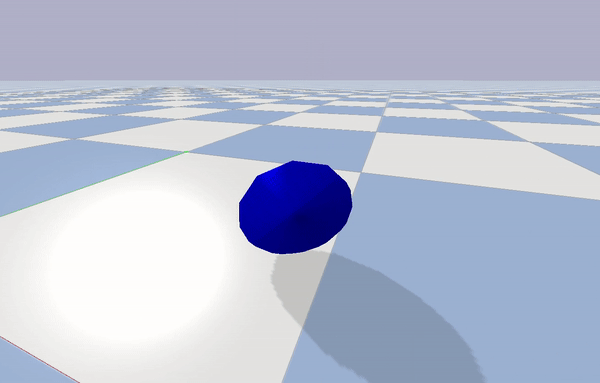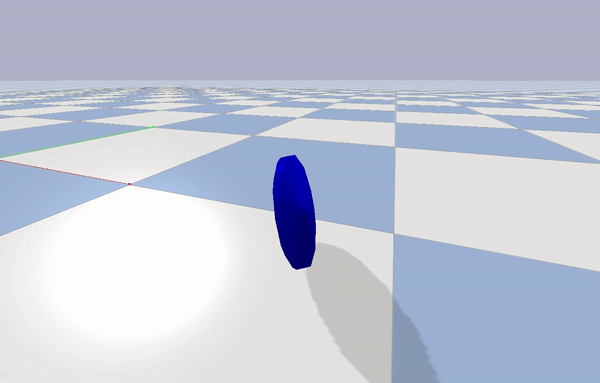
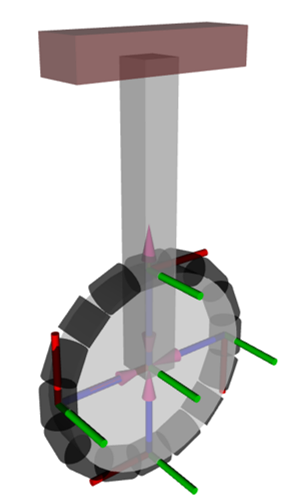
I first analyzed this phenomenon on a simple coin (Figure 1) rolling down a surface and extended my analysis to OmBURo (Figure 2). Check out my publication for more indepth derivations on the dynamics.

Cascaded Multi-loop Controllers

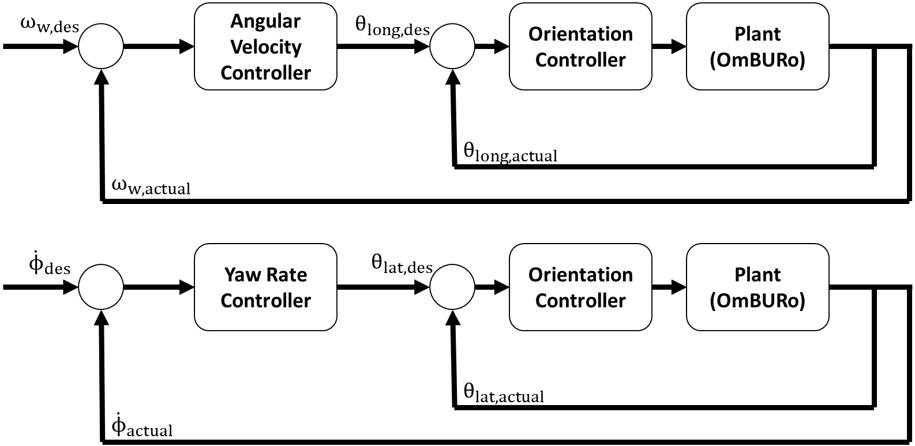
The dynamic analysis of the models shows a relationship between the angular velocity of the wheel, roll, and yaw rate of the body. The yaw rate can be controlled by maintaining a constant wheel angular velocity and regulating the roll. As balancing needs to be simultaneously regulated, a cascaded multi-loop control architecture is used as seen in Figure 3 (Top) to control both wheel angular velocity and pitch. The yaw rate and roll are controlled using the same control structure as seen in Figure 3 (Bottom), but with different gains. All the controllers are PID and PI controllers.

Results and Discussion

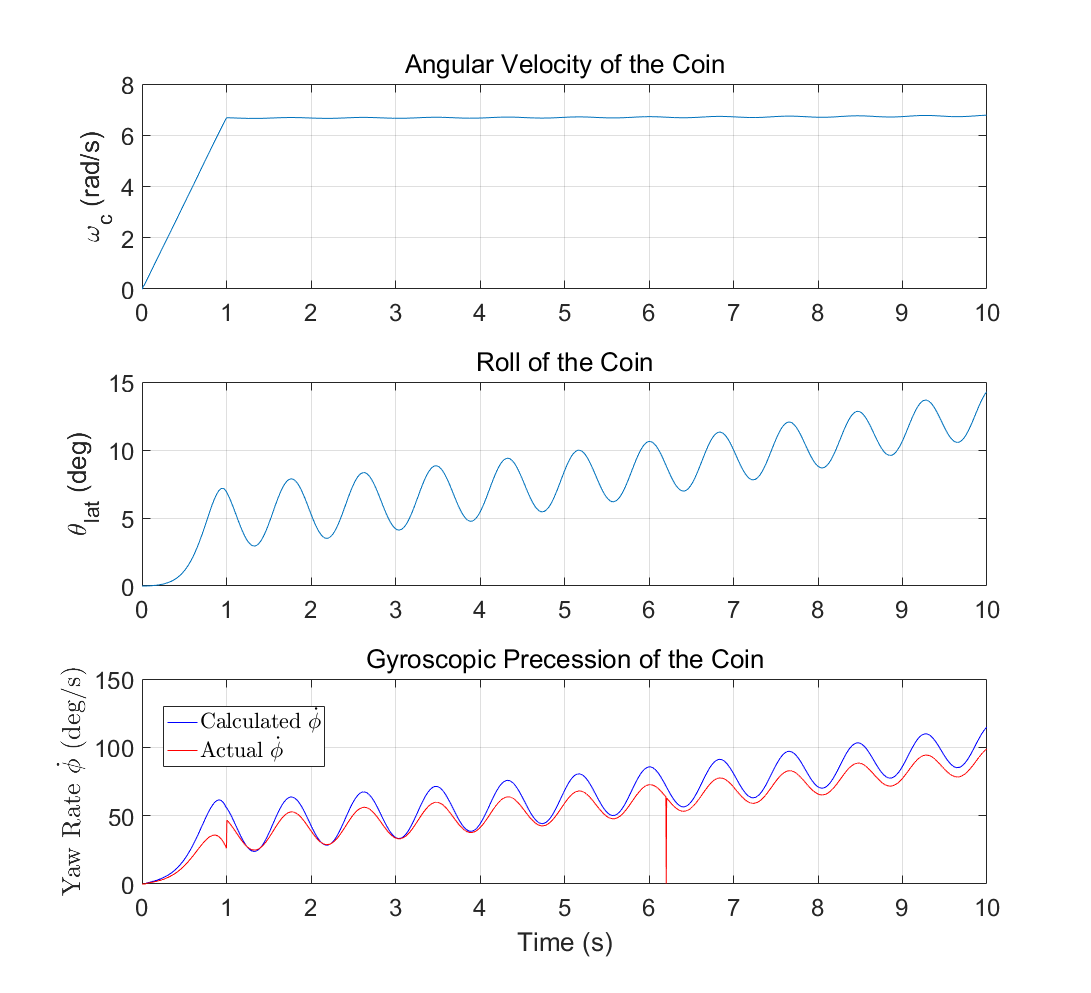
First a simulation of a coin rolling was built to verify the dynamic analysis. Below is a simulation of a coin in PyBullet, where the coin was accelerated for one second and then only affected by gravity afterwards. Figure 4 (Bottom) validates the theoretical derivation of the coin’s precession.

A simulation of OmBURo was built to repeatedly test and assess the feasibility of the approach (Figure 5). An environment was built using Pybullet.

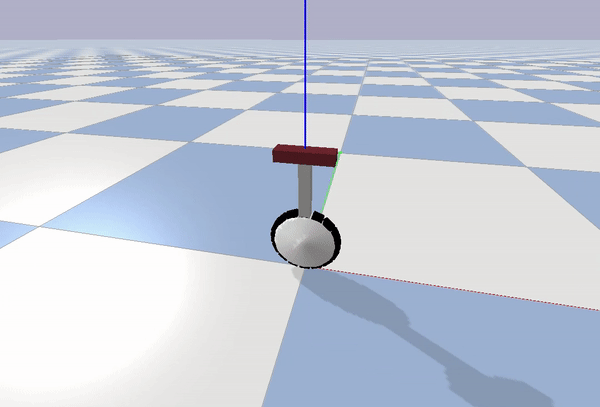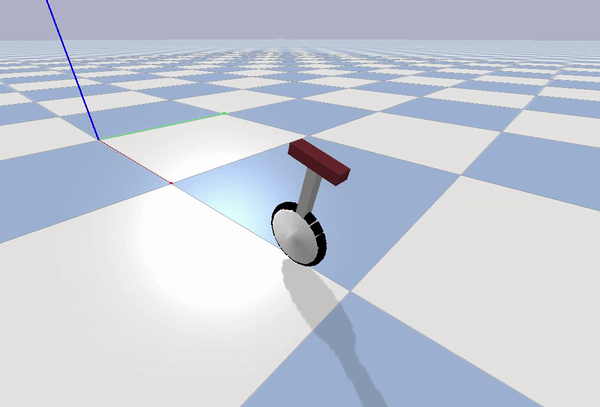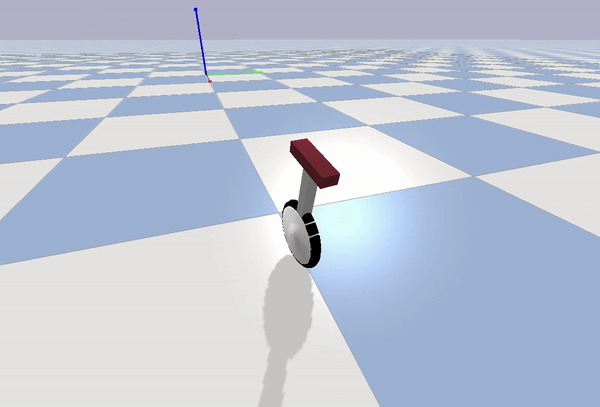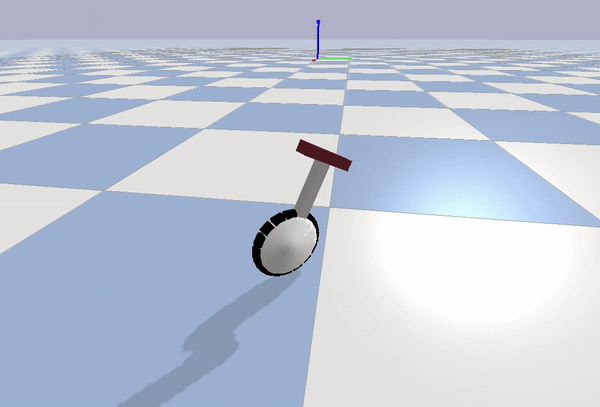
Gaussian white noise was added to the actuator and IMU readings to mimic the hardware as best as possible. The timestep of the simulation was set to 1/240. Due to the limitations of the simulation, there is a key difference in the actuation approach compared to the hardware implementation. Rollers and the wheel are driven separately unlike in the hardware implementation which uses a differential drive method to run the wheel and motors.

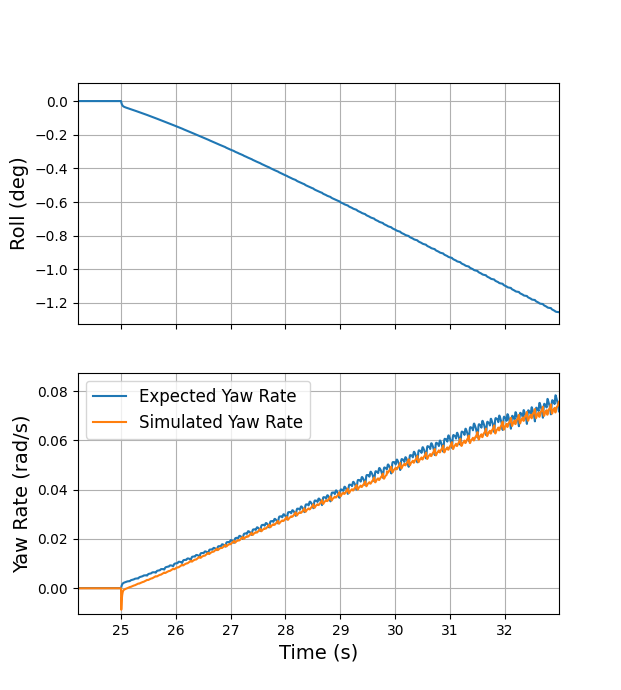
To begin with, to verify the derived dynamics of OmBURo’s gyroscopic precession, an expected yaw rate calculated using OmBURo’s yaw rate relationship is compared to the ground truth yaw rate from the simulator. OmBURo is commanded to track a given desired longitudinal velocity and roll orientation to collect sensor data to calculate an expected yaw rate based on OmBURo’s yaw rate relationship. When compared to the ground truth yaw rate as seen in Figure 6 (Bottom), the results clearly show that the derived dynamics are sufficient for describing OmBURo’s gyroscopic precession.

To reach a given desired yaw rate, as precession is a function of angular momentum, it is important to first be able to track a desired wheel angular velocity. Figure 7 (Bottom) shows a reference wheel angular velocity, which the proposed cascaded controller tries to track. Note that the actual angular velocity is decided based on robot’s pitch orientation. Hence, the wheel angular velocity controller feeds the reference pitch angle to the orientation controller, which when tracked well, will result in the desired angular velocity. We can see that the resulting wheeled angular velocity is tracked well. Interesting to also note is that like other unicycle robots, an initial retrograde can be observed at 2 seconds in the wheel angular velocity when given a desired pitch.

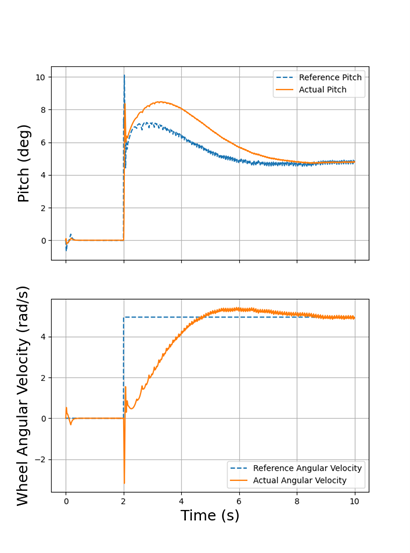
Once a steady wheel angular velocity is maintained, the yaw rate controller is turned on to track a given rate as seen in Figure 8 (Bottom). Rather than an instantaneous increase to some non-zero desired yaw rate, a ramp reference is given to avoid causing unnecessary instability to the system. We can see from the results that the cascaded yaw rate controller is able to track a given reference yaw rate.

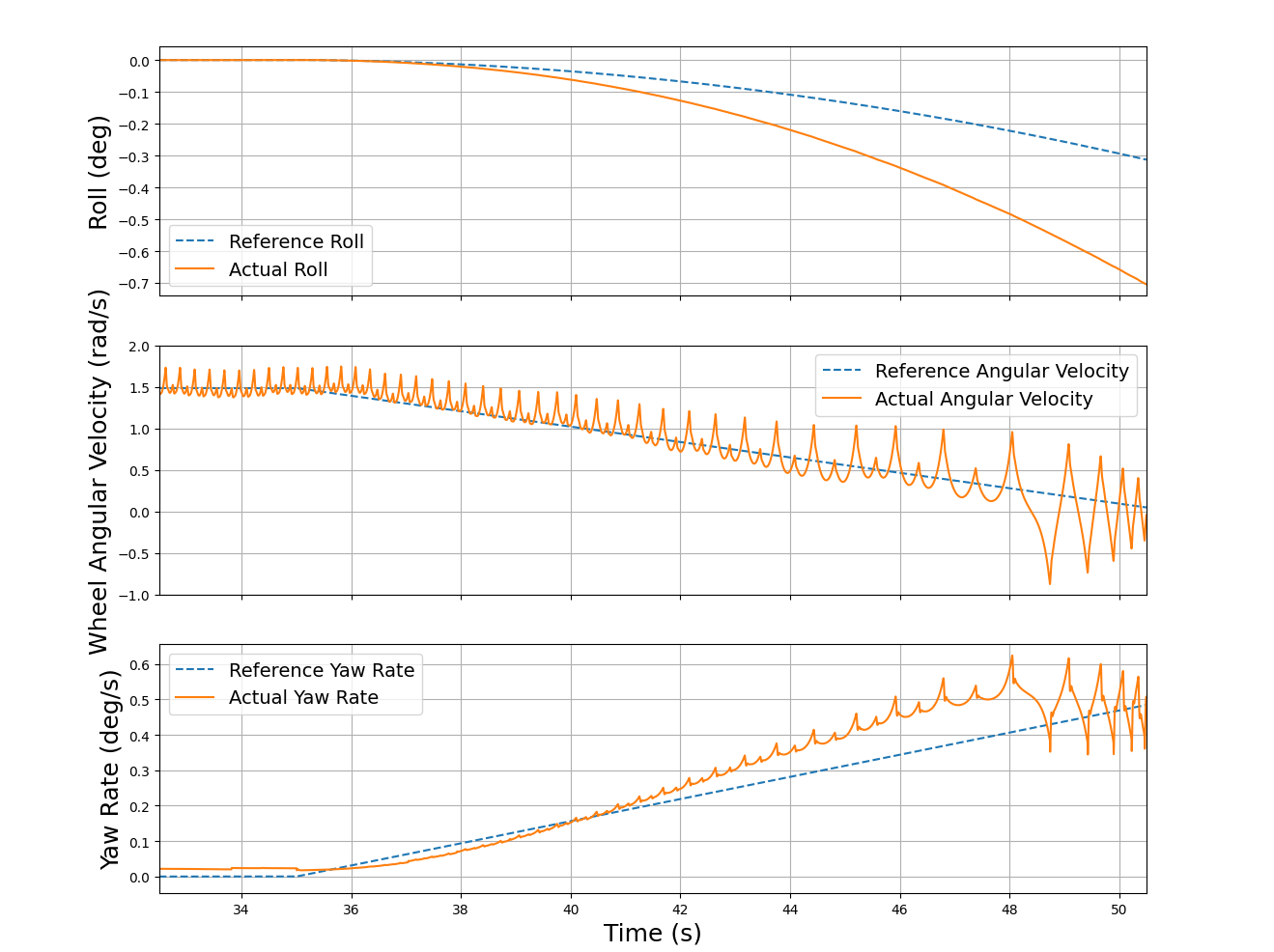
However, note that at higher angular velocities, there are limitations with a simple PID approach due to the inherent mechanical configuration of the platform. Because OmBURo is able to move omnidirectionally, its complex coupled dynamics make it much more sensitive to the fluctuations in the variables than conventional unicycle robots. Hence, though the general shape of the desired yaw rate is achieved, when moving faster, the desired yaw rate is not accurately tracked as seen in Figure 9 (Bottom).

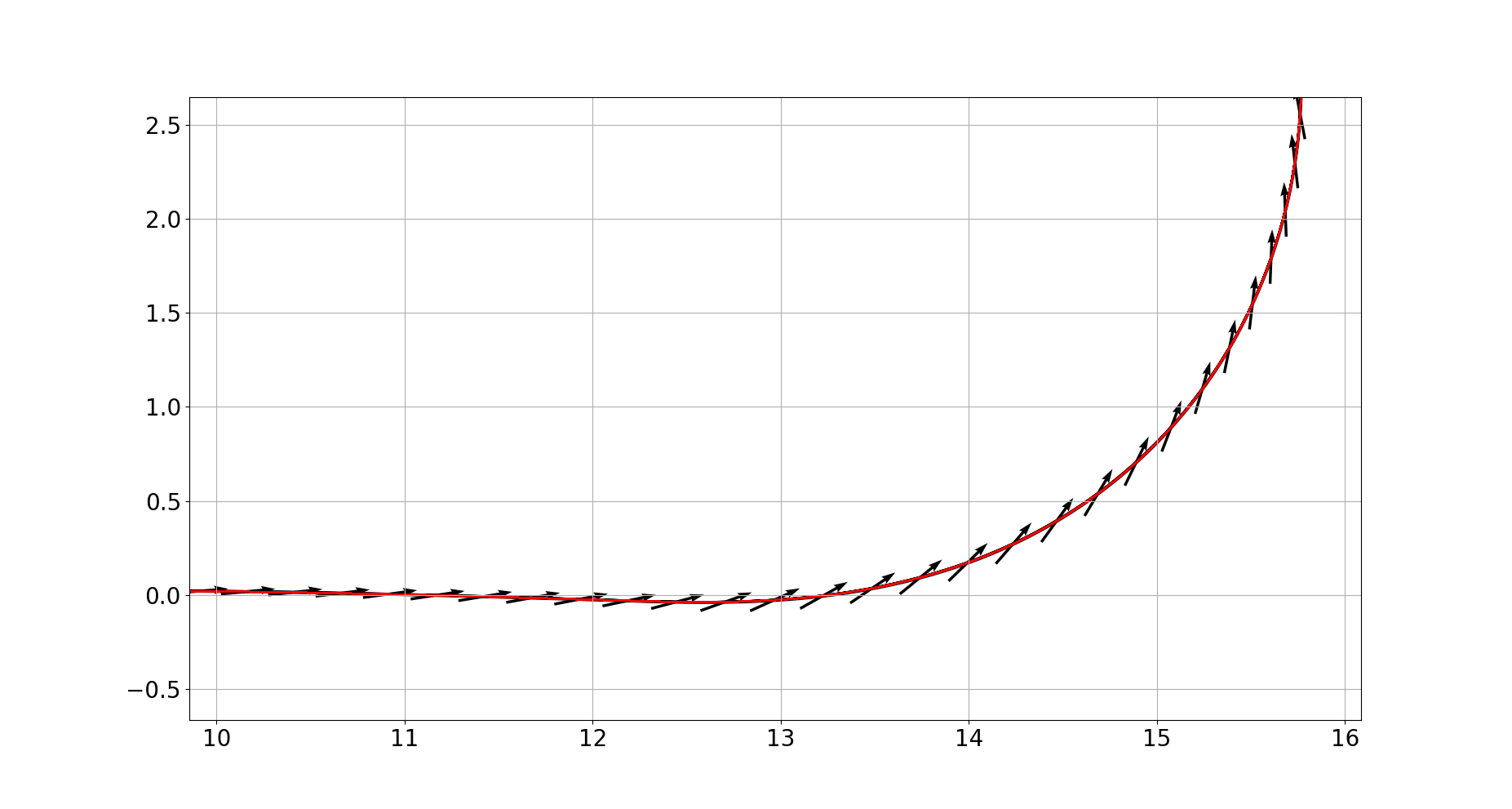
Additionally, a key difference between OmBURo and conventional unicycle robots can be observed during faster turns, where OmBURo “drifts” like a car. As seen in Figure 10, OmBURo’s trajectory is unlike that of a conventional unicycle robot, where they are required to be facing the direction they are traveling. While on this path, the force balance performed on the roller in contact with the ground in the lateral direction reveals that centrifugal forces are only partially countered by friction. Part of the centrifugal forces are balanced by the angular acceleration of the rollers. The increase in roller angular velocity affects the yaw rate. Consequently, the increase in yaw rate produces a larger centrifugal force, causing more roller angular acceleration. Hence, OmBURo is destabilized by this cycle of coupled dynamics, making yaw rate tracking difficult, and eventually will fall down.

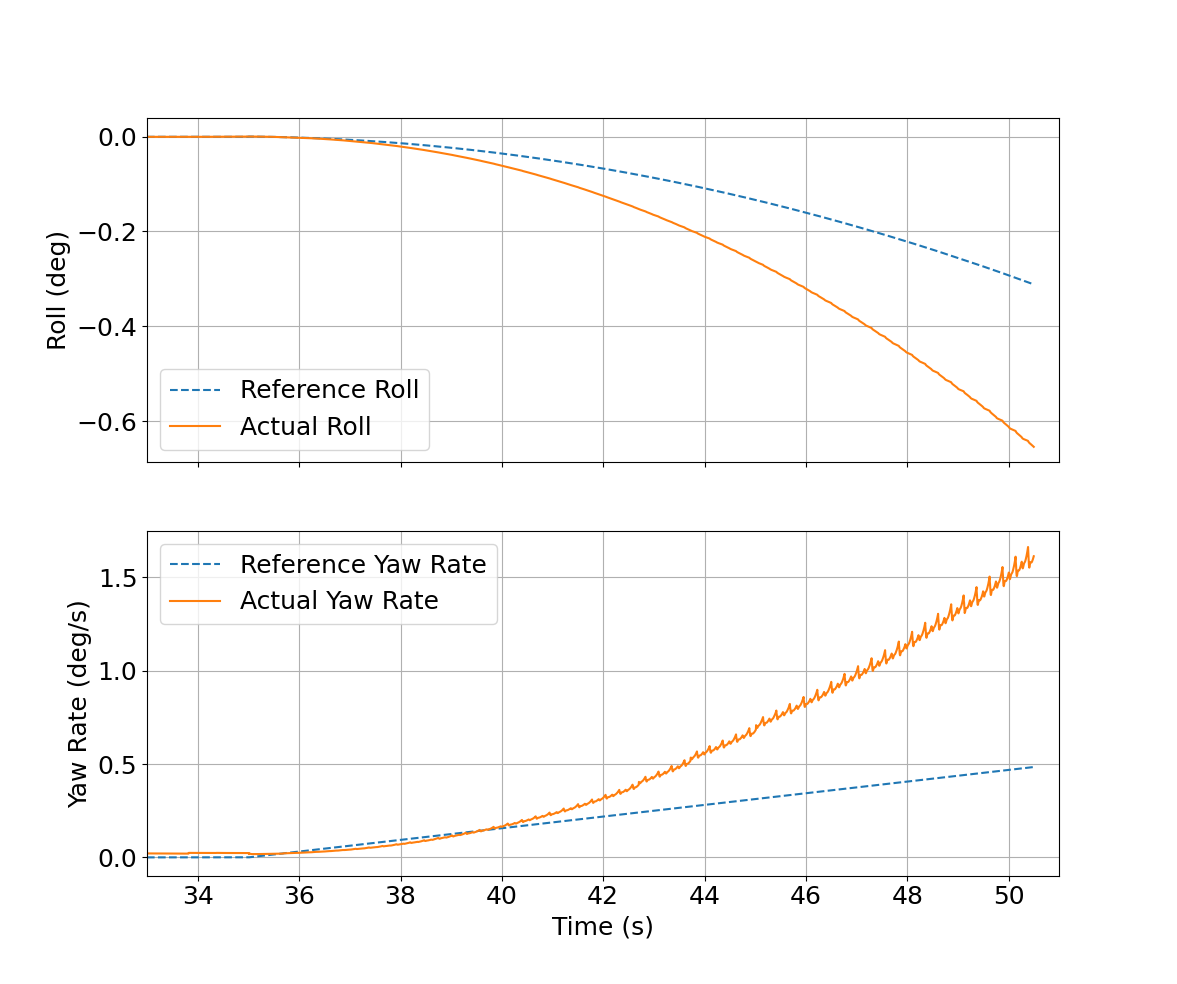
The reason the proposed approach may still work at lower velocities is because of torsional friction force helping lessen the problems caused by the cycle of coupled dynamics, even though the dynamics derived indicate that a decrease in the wheel angular velocity would increase the yaw rate. The gradual decrease in angular velocity seen in Figure 8 (Middle) helps dampen the yaw rate even though the roll seen in Figure 8 (Top) is very similar to Figure 9 (Top). By making the angular velocity reach zero at the end of a commanded reference yaw rate effectively stops OmBURo from turning, as gyroscopic precession is no longer valid.

Additionally at this point, the aforementioned drift could also be addressed. The roller angular velocity controller can be activated to address drift with minimal change to the yaw state as the robot is no longer moving longitudinally. This would eventually let OmBURo instantaneously come to a stop, bringing OmBURo back to a state where it can again track a given yaw rate to reach a final desired yaw. Note that dealing with drift during turning is a unique behavior that exists due to OmBURo’s mechanical design and a different approach to address it could also be developed and appended after the proposed yaw rate controller.